[Lab seminar] The graph neural network

논문원본
Franco Scarselli Marco Gori; Ah Chung Tsoi; Markus Hagenbuchner Gabriele Monfardini

Introduction

• graph : 노드와 간선을 모아놓은 자료 구조로, 객체와 객체간의 연결 관계를 표현 할 수 있음
• 머신러닝에서, graph의 node를 실차원의 vector(target)로 mapping 시키는 함수를 학습시키는 것
• graph응용의 종류
  • Graph focused
    • 그래프 전체를 보는 응용
    • ex) 화학 화합물
  • Node focused
    • 그래프의 노드 하나하나를 중요시 보는 응용
    • ex) image object detection
• 이전의 machine learning에서 그래프의 사용
  • 그래프의 node정보를 벡터로 변환한 후에 사용함 -> 노드들간의 연결관계 정보가 손실됨.
• RNN, Random walk/Diffusion model을 확장해서 그래프 structure을 직접 다루어 학습하도록 함

The graph neural network

Notation

• positional graph -> 노드n의 각 이웃(u)에 고유한 정수 식별자를 할당하여 이웃간에 구별이 될 수 있도록 함
• non-positional graph -> 이웃간의 구별이 없음.

$$\mathcal{L} = \{(G_i,n_{i,j},t_{i,j})|G_i=(N_i,E_i)\in\mathcal{G}; n_{i,j}\in N_i, t_{i,j}\in \mathbb{R}^m,1<i<p,1\le j\le q_i\}$$

• $\mathcal{D}=\mathcal{G}\times\mathcal{N}$
• $t_{i,j}$는 $n_{i,j}$의 target값

A. Model

• 노드와 주변의 정보를 기반으로 state를 정의 state : $x_n\in\mathbb{R}^s$
• $f_w$ : local transition function
• $g_w$ : local output function
• non-positional graph는 이웃간의 구분이 없으므로, 각각의 이웃을 포함한 state들의 합이라고 할 수 있음.
  

  

• input : graph, output : 실 값(vector등)
• input 과 output을 mapping 하는 $\varphi$를 구하는 것이 목적
• Banach 고정점 정리가 방정식의 해법의 존재와 고유성에 관한 조건을 제공
  • $F_w$가contraction map인 경우 유일 해를 가짐
  • $^\forall(x,y)에 대해 ||F_w(x,l)-F_w(y,z)||\leq\mu||x-y||$
    

    

B. Computation of the state

• $F_w$가 contraction map이므로 절차적으로 쓸 수 있고, x가 수렴함도 보장됨.

C. The learning Algorithm

• GNN의 학습은 $\varphi$가 학습데이터 셋에 근접하도록 parameter w를 추정하는 것.
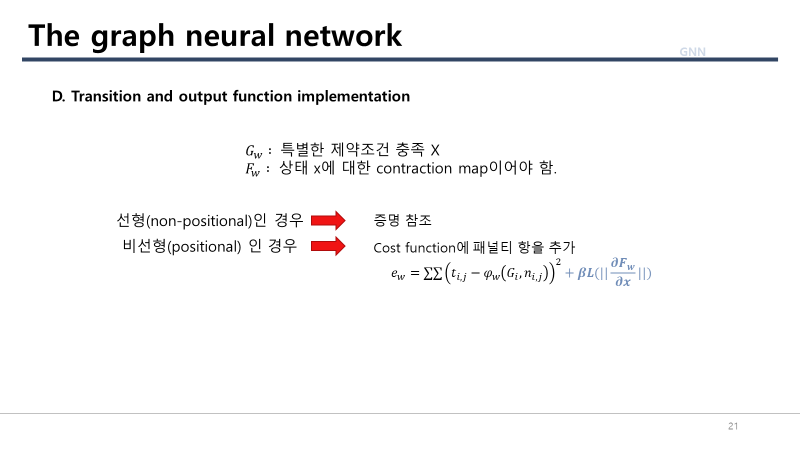
• cost function은 모델의 다른 속성을 제어하는 패널티 항을 포함할 수도 있음.
  • 나중에 $f_w$에 대한 제약조건을 만족시키기 위해 costfunction에 패널티항을 포함함.

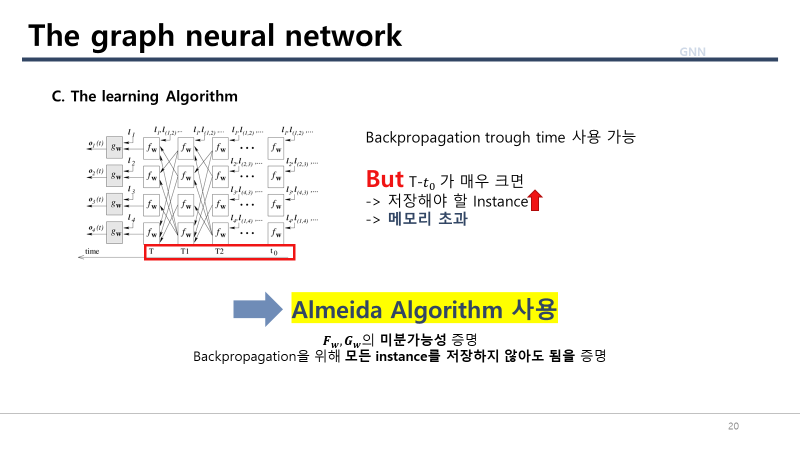
• T-$t_0$가 너무 크면 저장해야할 Instance의 상태가 너무 많아 메모리 초과로 구현 할 수 없음
• 이를 해결하기위해 almeida algorithm을 사용함.
  • 미분 계산전에 $x_n^t$가 안정적인 점 x에 도달하여 $x^t=x$가 $t\geq t_0$에 대해 유지된다고 가정 가능
  • backpropagation through time은 x만 저장함으로써 수행될 수 있음.

1. 미분 가능성(Differentialbility)
   • $F_w,G_w$ : gnn의 global transition/output function
   • $F_w,G_w$가 x,w에 대해 연속이고 미분가능하다면 $Q_w$도 w에 대해 연속이고 미분 가능함

증명

$\theta(x,w) = x-F_w(x,l) \theta$를 정의
$ ||\frac{\partial\theta}{\partial w}|| = I_a-\frac{\partial F_w}{\partial x}\geq(1-\mu)$
$\frac{\partial\theta}{\partial x}$의 determinant$\neq$null
$\theta$와 w사이에 implicit function theorem을 적용함
$\theta(\psi(w),w)=0, \psi(w) = F_W(\psi(w),l)$
$\rightarrow$ w의 근처에서 연속이고, 미분가능한 $\psi$가 존재. 그리고 이는 모든 w에 대해 유지됨.
$rightarrow \psi$는 모든 도메인에서 연속적으로 미분가능함.
$\varphi(G,n) = [G_w(\psi(w),l_n)]_n$ : $\varphi_w$는 미분가능한 함수의 구성임

2. Backpropagation
   • $z^t\triangleq z^{t+1}\frac{\partial F}{\partial x}$라고 정의
   • $z^T,z^{T-1}...$은 $z = \lim_{t\rightarrow \infty}z^t$에 수렴
   • $\rightarrow \frac{\partial e}{\partial w} = \frac{\partial e_w}{\partial o}\frac{\partial G_w}{\partial w}+z\frac{\partial F_w}{\partial w}$

증명

너무 길어 이미지로 대체

D. Transition and Ouput Function Implementations

E. A Comparison with random walks and recursive neural networks

• GNN은 다른 모델의 확장임
  • RNN은 GNN의 특별한 경우임
    1. 입력 그래프가 방향 비순환 그래프
    2. $f_w$의 입력이 $l_n,x_{ch[n]}$으로 제한됨. ch[n] : n의 자식 집합
    3. 다른 모든 정점에 도달할 수 있는 방향 그래프의 정점인 super source 노드 $s_n$이 있음. $\rightarrow O_n$에 사용
  • $f_w$를 선형함수로 쓸때 Random walk도 캡쳐함.

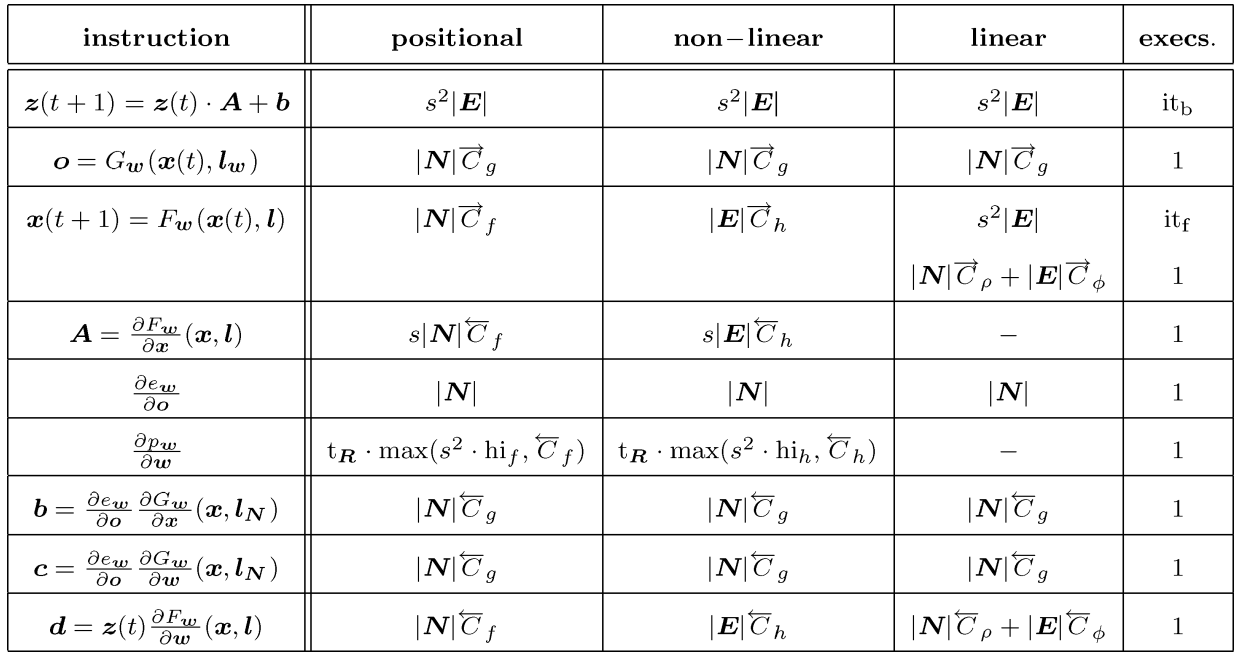
Computational Complexity Issues

Experimental Result

실험 환경

• matlab7
• 2GHz PowerPC Power Mac G5

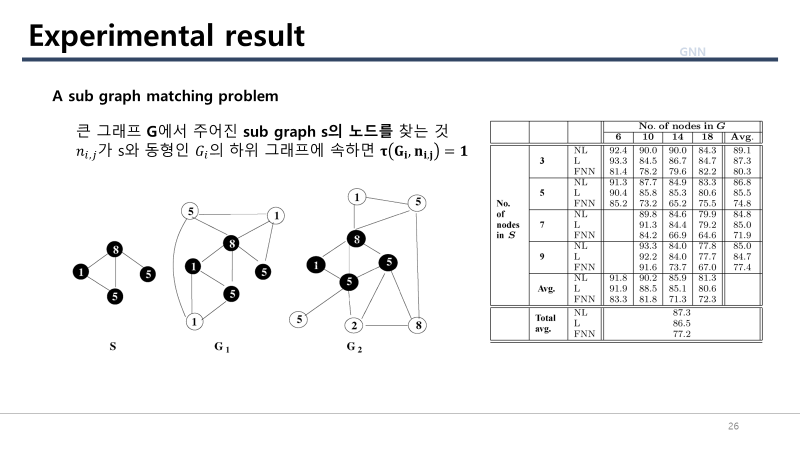
A sub graph matching problem

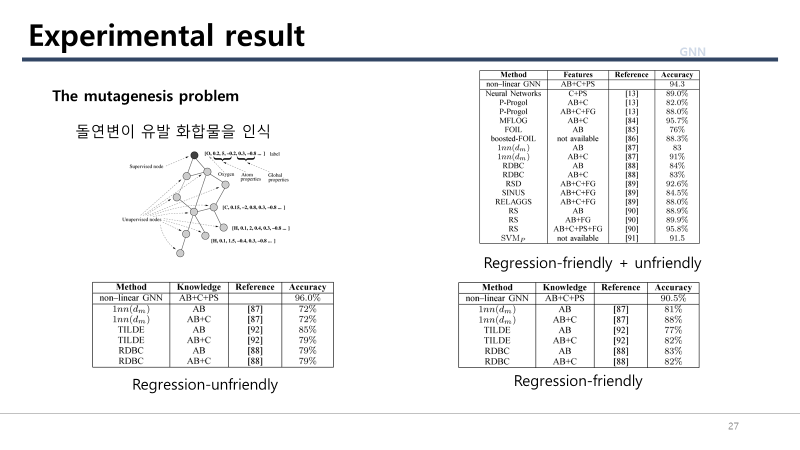
The Mutagenesis Problem

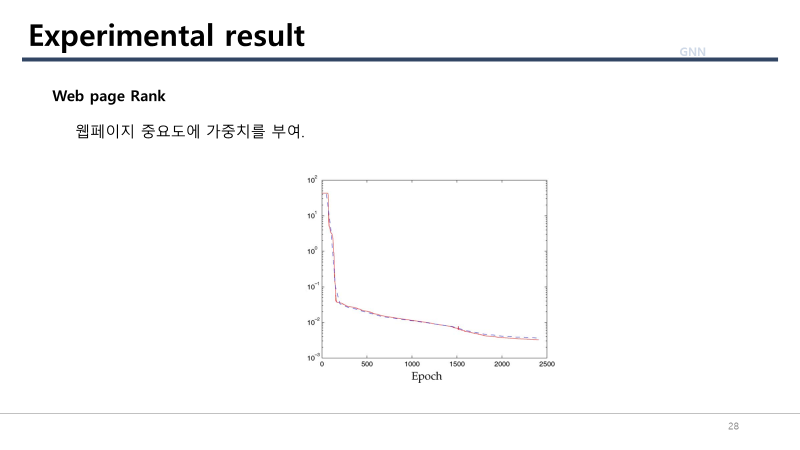
Web page Rank

Conclusion